どうも塾長です。
8月末に行われた全県模試の結果が返却されました。
受験した生徒たちには結果を順次返却中です。
今回の模試の結果は、ぶっちゃけ気にする必要はありません!
理由は、夏期講習では徹底した基礎基本の総ざらいしかしていないからです。
基礎基本の定着までできたら、自然と実力テスト系の成績は上がってきます。
冬が本格的に始まるまでは、応用問題に取り組みつつ、頭の使い方を意識して、基礎基本の抜け漏れを潰しながら丁寧に進めてください。(上位校志望者のみ。中堅校志望の場合は、引き続き基本的な知識のインプットをメインに進めてください)
ここでいう基礎基本の定着とは、基本事項を自由自在に操れる状況にあることです。
問題集の基本問題が◯になる=基礎基本が定着している
と見てしまうのは大きな誤りです。
以下昨年の愛知県の問題からの抜粋です。
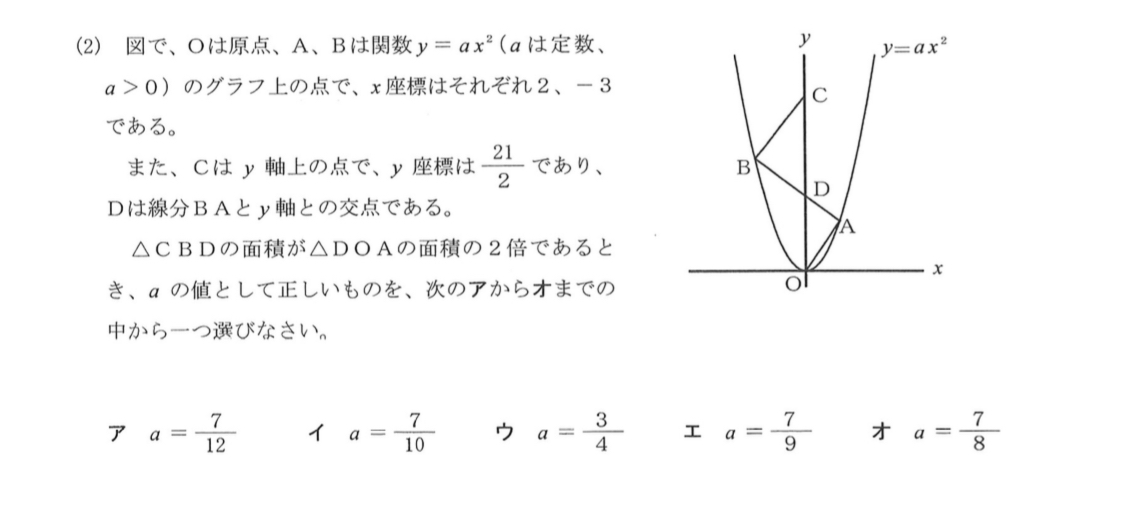
この問題を見て、いきなり答えまでの道筋が浮かばなくても良いですが、
「とりあえずAの座標は(2,4a)、Bの座標は(-3,9a)だな」
「△CBDの面積が△DOAの面積の2倍とあり、それぞれの高さは3と2だから底辺の比が何対何かわかるな」
このくらいまでは30秒で辿り着いてほしいところです。
一つひとつで考えていることは、基本中の基本です。
「y=ax^2のグラフで、x座標が2である時のy座標はどのように表せますか?」
などと直接的に問われなくても、このような問題中でスピーディに使いこなせることが、基礎基本が固まっている状態です。
ゆえに進学塾xの指導方針は、とにかく基礎基本の徹底、正しい思考プロセス、ここをまずは鍛えます。
上っ面だけで回答を作るような小手先のテクニックに頼っているようでは、応用問題に太刀打ちができません。
例えば、「y=3x^2のxが2から4まで増加するときの変化の割合」
を「a×(増加量の和)」で導き出すとか、大っ嫌いです笑
関数系の単元はとにかくグラフ書いてイメージ!
これに尽きます。
単なる感情論っぽく聞こえるかもしれませんが、理由もちゃんとあります。
目先の問題で丸になる方法だけを求めだすと、試行錯誤して答えを導き出すようなムーブができなくなります。
長考、熟考の類ができないと、その後の伸びは見込めません。
反射的に解ける問題の方が少ないですから。。
(だから小学生の「はじき」「くもわ」の指導法も本当に嫌いです。
それに頼り切ってしまった子は、
例えば、「時速30kmで5分走ると何km進みますか?」
に対して「速さ×時間で距離が出るから、30×5=150km!」
みたいな答えを平気で出すようになってしまいます。)
「なぜだろう?」「どうしてだろう?」
ここ抜きにして真の理解はあり得ません。
そして夏期講習のメインテーマはここでした。
基礎基本が自分のものになっていないと、実際の入試問題対策に入った時に、ちゃんと伸びません。
入試対策は基礎基本がガッチリ固まっていれば3ヶ月で十分です。
つまり12月に入るタイミングですね。
それまでが基礎基本を固めるリミットです。
もうひとつ例を出すと中2の一次関数の変域の問題。
「何でか知らんけど、xの変域の端と端を代入しとけば、yの変域は出るよね〜」
とりあえずそれで定期テストは◯になりますが、xやyの変域に文字が混ざってくるような応用問題で詰みます。
とにかく関数はグラフを書いて考える。
変域とはそもそもなんぞや?グラフ上でどのように表現されるんだ?
増加量と値の違いってなに??
そんなことは直接的に聞かれませんが、
上記のようなことがわかった上での◯なのか、
理屈は知らんけど、そうやれば答えが出るよね程度の認識で◯なのか、
前者は実力系テストでも力が発揮されますし、後者は実力系テストがボロボロになります。
入試はもちろん実力系テストに分類される訳ですから、目先の問題がとりあえず◯になればいいというのは甘すぎます。
意外とここを軽視してしまう子が、学年上位10〜30%付近にはたくさんいると思います。
学年上位10〜30%くらいにいれば、まぁまぁできる子の分類かと思いますが、そこからもうひと伸びしたければ、やはり「基礎基本を自由自在にかつスピーディに操れるまで理解と演習を積む」のが欠かせません。
わかりやすく言えば、
「なぜだろう?」「どうしてだろう?」と疑問を常に持ち、
それに対する回答を自分の言葉で、スムーズに説明できること。
そうなるまで練習を繰り返すこと。
これを徹底してください。
ある程度成績も伸びたけど、中の上、上の下くらいの成績で伸び止まってしまっている子、ここに更なる飛躍の鍵があります。
今まで瞬間的に答えを出すだけの勉強しかしてこなかった子にとっては負荷が強い話ですが、
成長には負荷が必要です。
基礎基本を侮ること勿れ。
それでは!
