どうも塾長です。
最近、LINEで送られてくる質問対応と、授業で1日が終わってしまい、ブログに手がつけられていませんでした。
というわけで、前回の続きから。
前回の記事で
「発想力」とは「基礎基本を高速で試行錯誤できる力」「複雑な状態のものから、シンプルな部分を抽出する力」と言い換えることができる。
と書いたのですが、この部分を具体的に問題を解きながら、詳しく説明できればと思います。
あと、これだけは初めに申しておきたい。
発想力が必要になる難問は
解説を見て答えまでの過程を理解することより、
「どうやってその解き方を思いつくのか?」を明確にする方が重要です!
だって答えに至る道筋を理解できても、本番当日、その発想が生まれなかったら意味ないですよね??
つまり、発想をすること(=解き方を思いつくこと)を、感覚に頼るのではなく、再現性を持てるようにしておくのです。
これが最強です。
進学塾xは授業でこの部分をかなり重視しています。
常に生徒が本番で力を発揮できるように、「生徒自身が再現性が持って本番に挑めるための授業」を実施しています。
自塾の宣伝で失礼しましたが本題へいきましょう。
昨年の愛知県公立高校入試、数学の問題を使います。

(1)複雑な状態のものからシンプルな部分を抽出する
(2)基礎基本を高速で試行錯誤する
を2つに分けて説明します。
問題の①は簡単なので割愛します。
(1)複雑な状態のものからシンプルな部分を抽出する
まず一番初めにすべきことは「何を求めるか」を明確に把握することからです。
今回は面積を求めるべきなので、画像の通り、3パターンのいずれかで求めていくことになりそうです。
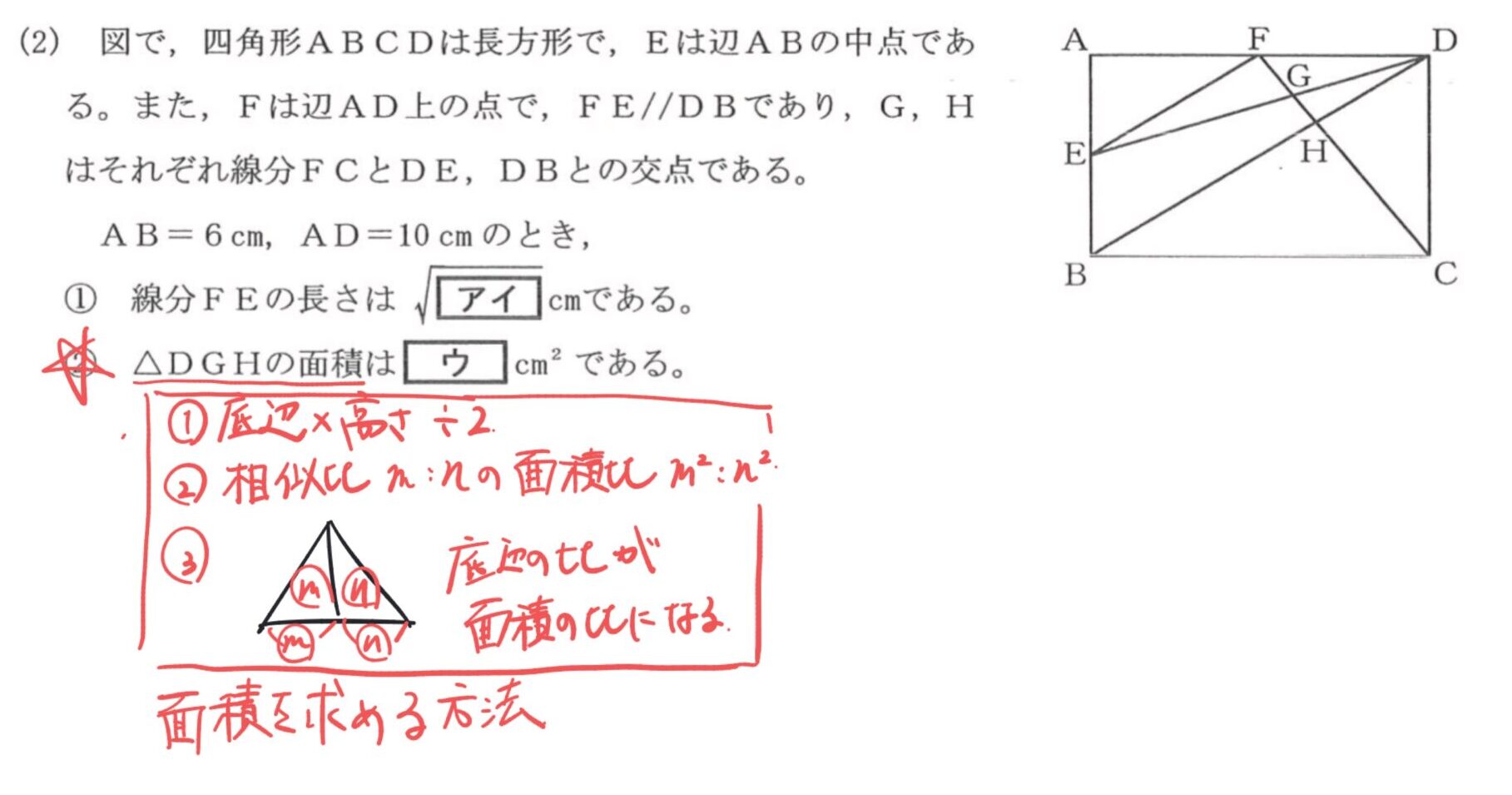
そして、△DGHを3パターンに絡ませ、問題文の条件も併せて図形をみていくと、以下の2枚の画像内の形が見えてきます。
(他にもあるかもしれませんが、塾長がパッと見えたもののみで考えていきます。)

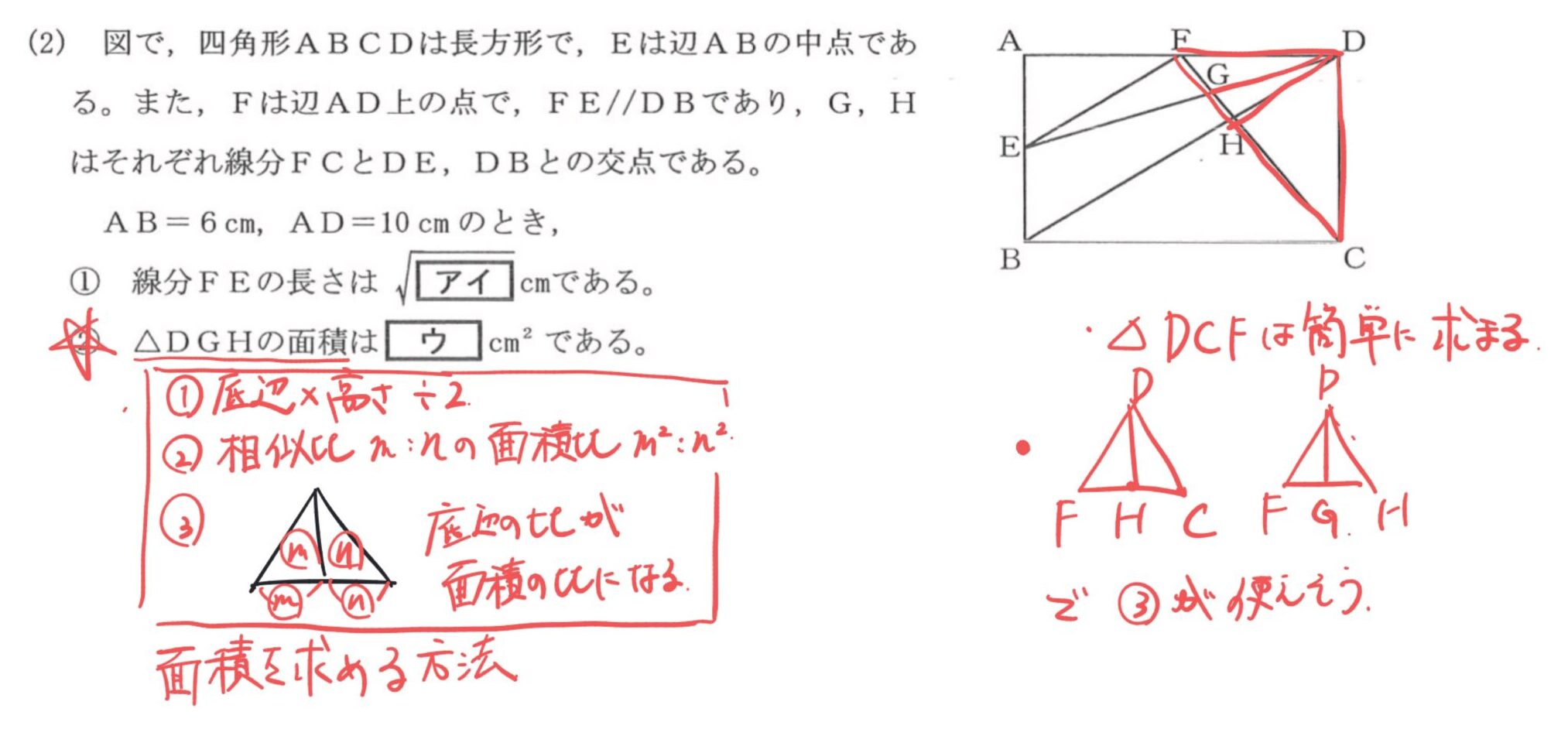
こんな感じで、求めるべきものと、その求め方のパターンを併せて考えながら図形をみて、パターンに当てはまる形を抽出していきます。
(2)基礎基本を高速で試行錯誤する
では続いて試行錯誤を行っていきます。
ここでも抽出の考え方は使いますが、試行錯誤の部分に焦点を当てて説明を進めます。

まずは、この考え方で問題を解くためには、
①FG:GHの比を出すこと
②△FGHか△FDHの面積を求めること
が必要になります。
①のFG:GHを求めるためには、、、
△FHDに注目しているだけでは、出てきそうもありません。
というわけで、この考え方はボツです。
ではこの考え方はどうでしょう?

この考え方で問題を解くには
①△FDCの面積を出す(辺FDと辺DCの長さを出す)
②FG:GH: HCの比を求める
が必要になります。
①は余裕でクリアできますね。
FD=5cm
DC=6cm
なので、面積は15㎠です。
続いて②です。
線分の比を求めるには、以下の画像の方法をよく用います。(他にもありますが、ひとまず)
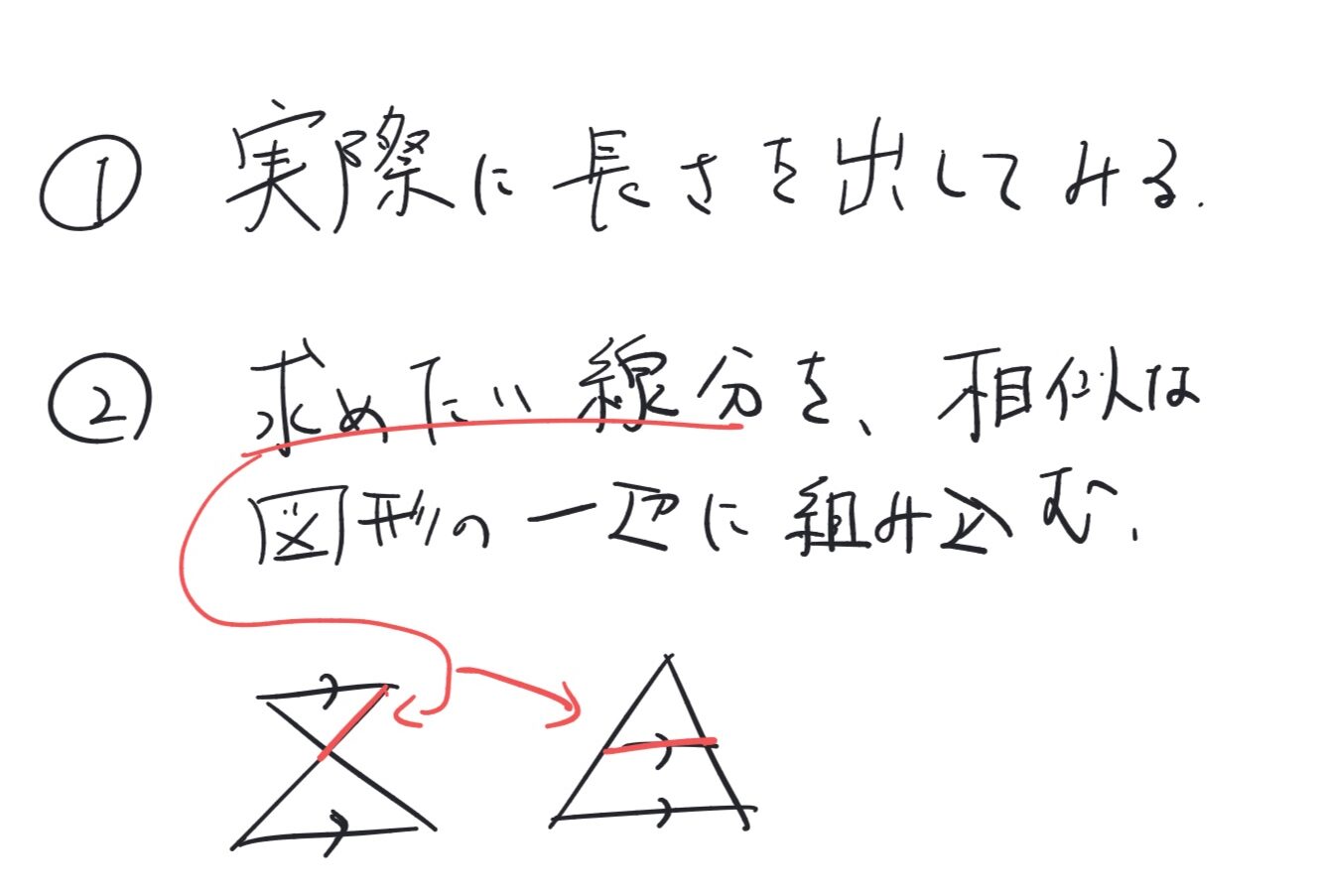
このように見ていくと、

FH:HC=1:2
がわかります。
続いて、
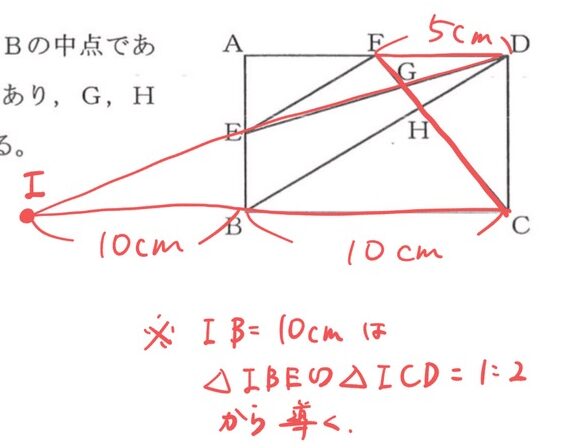
この話から、
FG:GC=1:4
ともわかります。
今求めてきた2つの比を組み合わせると、
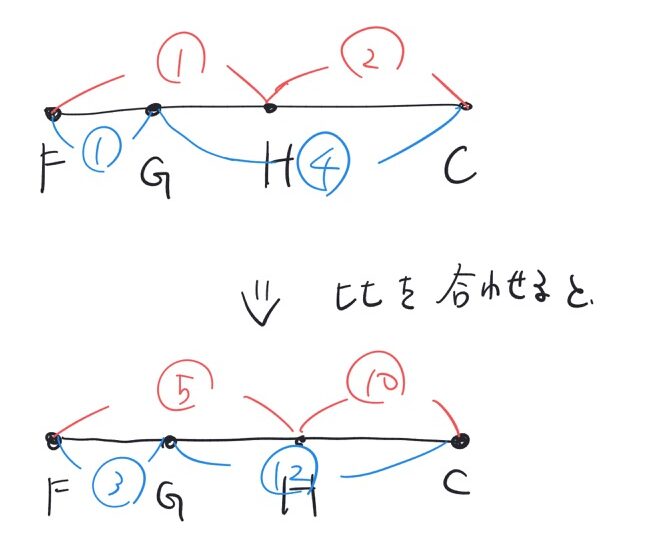
このように考えられますので、
FG:GH: HC=3:2:10
といえます。
あとは、面積の求め方③に当てはめて15㎠を縮めていけばクリアです。
まとめ
このように、「あーでもない」「こーでもない」というのを高速で行いながら、答えに辿り着けそうな解き方を探ります。
抽出や試行錯誤の際に用いた考え方は、一つ一つは超基本的な話です。
つまり、最後は「基礎基本」がモノを言う。
とも取れますね。
問題を見て、「今までに習った何が使えるだろうか??」という視点で試行錯誤を行うため、
これを実践でやるには、「基礎基本」の部分がスムーズに扱えるようになっておく必要があります。
●3つの相似条件
●中点連結定理=底辺とサイドの辺の中点を結んだ線は平行かつ2:1
●相似な図形の面積比はm^2:n^2
などなど、これらがスッと取り出せるようになるのがまずは目指すべきところです。
(答えに直結しようがしまいが関係なくです)
発想しやすくするための(=何が使えるかをスムーズに導き出すための)テクニック(?)もあります。
それは、わかっている辺や角の情報をとにかく書き出してみることです。
ジッと眺めているだけでは何も浮かびませんので、とにかく手を動かしてみることも大切です。
数学の最後の図形問題で伸び悩んでいる子の助けになれば幸いです。
長くなりましたが、この辺で。
